汽油价格排序_汽油价格统计

1.本福特定律 课程分享3 2022-04-16

2.油站中的91#92#是什么意思？

3.汽油石化好还是壳牌好

资料来源：美国劳工部颁布的统计消费价格指数（CPI），2008年4月；《WER》，2008。

由于欧佩克国家中的税收相对较低，所以零售价格远低于绝大多数发达国家的价格。

即使媒体上每天的头条新闻都有对创纪录的油价的哀叹，美国实际上还是全世界油价比较便宜的地区之一。根据对全球155个国家与地区的调查，若从最便宜的地区排序，美国的油价位于第44位。如2008年4月后期的情况，这种差异也是令人束手无策的，美国的汽油平均价格为3.45美元／加仑，而绝大多数欧洲国家的油价则超过了8美元／加仑。美国一直努力保持低油价，目前争论的焦点是方面如何努力使这种已令世人难以接受的油价保持在一个合理的水准。但是，这些便宜的油价——美国正在实施的油价对于其他国家来说却是可望而不可即的。而这种便宜的油价也诱使美国人陷入了不断购买大型轿车和更大住宅的循环中，似乎全球上涨的油价阴影距离美国人是遥远的事。

价格的比较也不能一概而论。跨国的油价比较，或以不同的交换律比较总是件难事。与欧元相比，美元已大大贬值。加之人们的居住远近不一，公交车就可派上用场，而缴纳高油价的人也会从其他方面受益，如欧洲拥有较强的社会保险网，包括较为便宜的健康保健和较高的教育水准，这些就有一些是纳税人所缴纳的油价中所含的税金。

本福特定律 课程分享3 2022-04-16

壳牌的汽油质量很好，壳牌的油比中石化和中石油更经用些，油的质量更好。

兰壳牌集团，总部位于荷兰海牙和英国伦敦，由荷兰石油与英国的壳牌两家公司合并组成。它是国际上主要的石油、天然气和石油化工的生产商，同时也是全球最大的汽车燃油和润滑油零售商。

它亦为液化天然气行业的先驱，并在融资、管理和经营方面拥有相当丰富的经验。业务遍及全球140个国家，雇员近9万人，油、气产量分别占世界总产量的3%和3.5%。作为荷兰最大的工业公司，其在2012年《财富》杂志世界500强中名列第1位。

扩展资料：

规模

荷兰/壳牌公司集团1996年取得了辉煌的业绩。一方面由于原油价格大幅上涨，公司集团抓住机遇，多产多销原油和油品；另一方面公司集团改组机构，加强管理，降低生产成本等措施也起了关键作用。

1996年壳牌集团销售额为1281.74亿美元，比上年增长了16.7%，在世界500家大公司中排名第6；实现净利润88.87亿美元，比上年增长28.7%，在世界500家大公司中排名第1；

至1996年底，公司资产总值1243.73亿美元，比上年增长了5.39%：股东权益631.27亿美元，比上年增长7.02%; 负债总额612.46亿美元，资产负债率49.24%，比上年下降了0.78个百分点。

19年上半年壳牌集团净利润为24.86亿英镑，比1996年同期下降了15.04%，主要是由于炼油和销售部门的存货损失造成的；至19年6月30日的12个月平均运用资本收益率为11.5%，比1996年下降了1.7个百分点。

壳牌集团1996年分部门销售情况和分地区销售情况分别见表1和表2。

1996年壳牌集团销售额大幅度上涨，比1995年增长了17.94%，比1992年增长了49.16%。其中炼油和销售部门销售额增长最多，1996年比1995年和1992年分别增长了21.25%和52.14%，勘探和开发部门则分别为25.73%和44.22%。

同时，壳牌集团在油气和化工以外的其他部门的销售额在逐年下降。从地区看，美国地区销售额增长最快，1996年比1992年增长了56.60%，其次是西半球地区。

百度百科-壳牌石油

油站中的91#92#是什么意思？

本福特定律 ? 课程分享 3

? 这是通识选修课《经济研究中的计算方法》第二讲中出现的案例。

? 本福特定律是一个非典型数字统计定律，它由来已久。虽未被广义的证明，却有着重要的应用。最直接的作用就是，它可以帮助侦破“数据”，在各个领域。

（一）本福特定律

? 本福特（Benford）定律，又称为第一数字定律。它是数字统计的一种内在规律，指所有自然随机变量，只要样本空间足够大，每一样本首位数字为1至9各数字的概率在一定范围内具有稳定性（见图）。即以1开首的样本占样本空间的0.3，以2开首的样本占样本空间0.17-0.19，而以9或8开首的样本始终只占0.05左右。

? 世界上千千万万的数据的开头数字是1到9中的任何一个数字，而且每个数字打头的概率本应该差不多，但如果你统计的数据足够多，就会惊讶地发现，打头数字是1的数据最多。?

? 1935年，美国的一位叫做富兰克?本福特（Frank Benford, 1883–1948）的工程师在图书馆翻阅对数表时发现，对数表的头几页比后面的页更脏一些，这说明头几页在平时被更多的人翻阅。再进一步研究后发现，只要数据的样本足够多，数据中以1为开头的数字出现的频率并不是1/9，而是30.1%。而以2为首的数字出现的频率是17.6%，往后出现频率依次减少，9的出现频率最低，只有4.6%。?

? 本福特开始对其它数字进行调查，发现各种完全不相同的数据，均有这个定律的身影。比如，约三分之一的住宅号码是以1作为其首个数字的。许多几乎没有任何共通性的领域也有相同的情况：比如道琼斯指数的历史数据、个人电脑中文件储存的大小排列顺序、世界主要河流的长度、报纸头版头条的数字及其它许多事情，都是符合的。

? 1961年，一位美国科学家提出，本福特定律其实是数字累加造成的现象，即使没有单位的数字。比如，设股票市场上的指数一开始是1000点，并以每年10%的程度上升，那么要用7年多时间，这个指数才能从1000点上升到2000点的水平；而由2000点上升到3000点只需要4年多时间；但是，如果要让指数从10000点上升到20000点，还需要等7年多的时间。因此我们看到，以1为开头的指数数据比以其他数字打头的指数数据要高很多。

（二）本福特

? 本福特本来是一个美国电气工程师，也是一名物理学家，在美国通用电气公司（GE）实验室里工作多年直到退休。这位工程师在50多岁的时候，迷上了一个与数字有关的课题。课题得到的结论便是现在我们所说的“本福特定律”。

? 事实上，本福特定律的最早发现者并不是本福特，而是美国天文学家西蒙?纽康（Simon Newcomb，1835.3.10-1909.7.11）。纽康于1877年成为美国航海天文历编制局局长，并组织同行们重新计算所有主要的天文常数，繁杂的天文计算经常需要用到对数表，但那个时代没有互联网，没有阿里云，对数表被印成书本，存于图书馆。细心的纽康发现一个奇怪的现象：对数表中包含以1开头的数的那几页比其他页破烂得多，似乎表明计算所用的数值中，首位数是1的概率更高，因此他在1881年发表了一篇文章提到并分析了这个现象，但没有引起人们的注意，直到54年之后的1935年，本福特又重新发现这个现象。

? 说来令人奇怪，科学定律的发现有时候来自于一些毫不起眼，小得不能再小的现象，本福特的发现便是如此：以1开头的数字比较多，这也算是一个定律吗？他发现这种现象不仅仅存在于对数表中，也存在于其它多种数据中，于是，他检查了大量数据而证实了这点。

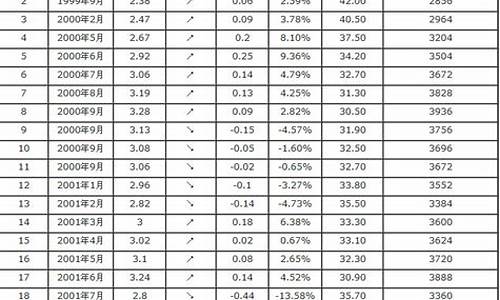
? 本福特对此疑问的观察要比纽康更深入一些。他开始对其它数字进行调查，发现各个完全不相同的数据，比如人口、死亡率、物理和化学常数、棒球统计表、半衰期放射性同位数、物理书中的答案、素数数字和斐波纳契数列数字中均有“第一数字定律”现象的出现。换句话说就是只要是由度量单位制获得的数据都符合这一定律。另一方面，任意获得的和受限数据通常都不符合本福特定律。比如，**数字、电话号码、汽油价格、日期和一组人的体重或者身高数据是比较随意的，或者是任意指定的，并不是由度量单位制获得的。

? 纽康发现这个定律的时间比本福特早了50多年，但很明显，后者是个更有心的人。否则就该叫做纽康定律了。

（三）本福特定律靠得住吗？

? 第一数字定律描述的是自然数1到9的使用频率，公式为F(d) = log[1 + (1/d)]（d为自然数）。人们分析后发现，由度量单位制获得的自然累加数据都符合第一数字定律，而任意获得的和受限数据通常都不符合。但人的身高、体重数据不符合，怎么解释？虽然定律在许多方面都得到了应用，但对于这类现象，人们依旧是迷惑不解。

? 再有就是怎么用数学方法证明定律，至今没有满意的结果。这是最大的问题，也是这个名头很大，叫做第一数字定律的本福特定律，至今无法进入数学或者统计学教科书的原因。

? 此定律的证明有不止一种，但都不严格。下面这个，虽然严格，但明显加了条件。

? 证明如下：设我们有一个很大的样本空间，有随机变量x?,x?,...,x_{n}，这里n足够大。x?,x?,...,x_{n}的演化规律可以用指数方程 来模拟。

? 如果我们对于指数定律的解两边取以10为底的对数，我们就会得到lg x(t)正比于时间t的结论。

? 如果我们问变量x介于80-90的概率有多大，我们只需要求出x(t=80)时t的解t?，和x(t=90)时t的解t?. 那么占总时间T的比率(t?-t?)/T即为x介于80-90的概率。

? 那么如果我们问首位数字是8的概率呢？多亏了duanx和zhuww的想法，我们只需要关心lg x的小数部分介于lg 8和lg 9之间的长度为多少即可。

? 这是由于关于10的对数lg x的整数部分决定着x是几位数（整数部分是1，说明是两位数；整数部分是2，说明是3位数……）。而lg x的小数部分则决定着x的每位数字是什么。

? 如果画一个lg x的小数部分关于时间t的图像，实际上就相当于把lg x的图像折叠到[lg 0,lg 10]区间。这样，我们就不需要关心时间T有多大，因为时间轴也被折叠了。那么首位数字为D的概率即为 [lg(D+1)-lg(D)]/(lg 10-lg 1)=lg(D+1)-lg(D)。

? 注意：上面的指数方程 是下面这个微分方程 的解。这个方程的物理含义是单位时间内，x(t)的变化量正比于x(t)在时刻t的值，比例系数为一常数k。

? 现实世界中，很多演化过程都可以用上边这个方程去近似，尤其是实在演化的初期没有达到饱和状态的时候。在维基百科上，我们可以找到很多这样的例子，比如关于指数衰减，指数增长，以及化学中的速率方程的降解部分。

（四）本福特定律的应用

? 不管如何诠释本福德定律，它是一个客观存在，并且是有用的。由于大多数财务方面的数据，都满足本福德定律，因此，它可以用作检查财务数据是否。

? 美国华盛顿州侦破过一个当时最大的投资案，金额高达1亿美元。主谋凯文·劳伦斯及其同伙，以创办高技术含量的连锁健身俱乐部为名，向5000多个投资者筹集了大量资金。然后，他们挪用公款用作自身享乐，为他们自己买豪宅、豪华汽车、珠宝等。为了掩饰他们的不法行为，他们将资金在海外公司和银行间进行频繁转账，并且人为账，给投资者造成生意兴隆的错觉。所幸当时有一位会计师（Darrell Dorrell ）感觉不对头，他将70000多个与支票和汇款有关的数据收集起来，将这些数据首位数字发生的频率与本福德定律相比较，发现这些数据通过不了第一数字法则的检验。最后经过了3年的司法调查，终于拆穿了这个投资，2002年，劳伦斯被判20年牢狱。

? 2001年，美国最大的能源交易商安然公司宣布破产，并传出公司高层管理人员涉嫌账的传闻。据说安然高层改动过财务数据，因而他们所公布的2001-2002年每股盈利数据不符合本福特定律。2001年12月，这个全球500强中排名第七的公司向美国证监会承认会计。安然引起公众对会计数据的关注，直接导致了2002年8月《萨班斯法案》的诞生。

? 美国税务局也利用本福德规则来检验报税表，揪出逃税漏税行为，据说有人曾经用此定律来检验美国前总统克林顿10年内的报税数据，不过没有发现破绽。

? 此外，本福德定律也被用于股票市场分析、检验选举投票欺诈行为等。

? 很显然，本福特定律是一个打击数据的大杀器。当然要注意它的应用条件：

1.数据不能是规律排序的；

2.数据不能经过人为设置；

3.数据量要足够大。有人说3000以上，不知有无依据；

4.它不是永远对，这是目前的未解之谜；

5.它是否准确，也有个标准问题，因为它更接近蒙特卡洛算法。

汽油石化好还是壳牌好

这是汽油标号！

汽油标号：是实际汽油抗爆性与标准汽油的抗爆性的比值。

标准汽油是由异辛烷和正庚烷组成。异辛烷的抗爆性好，其辛烷值定为100；正庚烷的抗爆性差，在汽油机上容易发生爆震，其辛烷值定为0。如果汽油的标号为90，则表示该标号的汽油与含异辛烷90%、正庚烷10%的标准汽油具有相同的抗爆性。 例如90号汽油，可以保证在压缩比不大于9的发动机上使用不产生爆燃现象，号汽油就可以保证在压缩比不大于9.7的发动机上使用不产生爆燃现象。标号越高，抗爆性能就越强。标准汽油是由异辛烷和正庚烷组成。但并不是标号越高越好，要根据发动机压缩比合理选择汽油标号。2011年12月，北京市拟定将汽油牌号由“90号，93号，号”修改为“89号，92号，95号”，并规定硫含量不得超过0.001 %。

我国传统意义上的汽油生产三巨头，向来有着“三桶油”名头的是：中石油、中石化、中海油（以油产量规模排序）。

长期以来，“三桶油”代表着国家石油的国标示范标准。至于网传的所谓“中石化原油靠进口，因此油品高于中石油”的说法，也是彻头彻尾的以讹传讹。因为我国主要从中东地区进口的原油，事实上也是低品级高含硫原油，并非是什么高大上的上品原油。

特别是从燃油环保等级进入国5阶段以后，事实上“三桶油”的汽油成品已经非常接近。至于壳牌石油在中国，是合资企业的形式，壳牌与延长石油合作出资。所以与国外的壳牌油品也是没有可比性的。中国的壳牌加油站的油品与“三桶油”其实差不多。

唯一的原则是：哪一家加油站距离单位或者家比较近，或者哪一家加油站优惠力度大，价格便宜就去哪一家。